Categorías: Artículos destacados » Electricistas novatos
Cantidad de vistas: 57937
Comentarios sobre el artículo: 4
Álgebra booleana. Parte 3. Esquemas de contacto
 El artículo describe los principios básicos del diseño de circuitos de relé de acuerdo con un algoritmo dado de su funcionamiento.
El artículo describe los principios básicos del diseño de circuitos de relé de acuerdo con un algoritmo dado de su funcionamiento.
En dos artículos anteriores me contaron lo básico Álgebra booleana y álgebra de relevos. Sobre esta base, se desarrollaron fórmulas estructurales y ya se desarrollaron circuitos de contacto típicos en ellas.
Elaborar una fórmula estructural de acuerdo con un esquema listo es una cuestión simple. Es mucho más difícil presentar el circuito eléctrico de la futura máquina de acuerdo con la fórmula estructural preparada. ¡Necesita algo de entrenamiento!
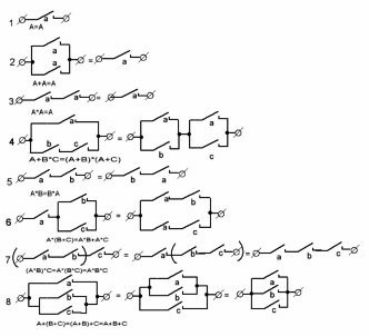
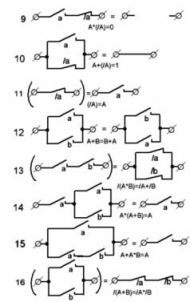
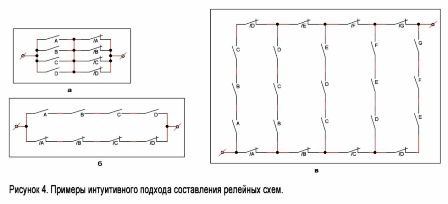
La Figura 1 muestra las opciones más comunes. circuitos de contacto y sus equivalentes. Ayudarán en la preparación de circuitos eléctricos de máquinas, así como analizarán estructuras preparadas, por ejemplo, durante el proceso de reparación.
¿Cómo puede usar las opciones para circuitos de contacto discutidas anteriormente?
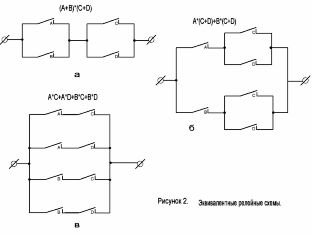
Considere el circuito que se muestra en la Figura 2, a. La fórmula estructural correspondiente tiene la forma: (A + B) * (C + D).
Usando la ley de distribución del álgebra booleana, abrimos los corchetes en esta expresión y obtenemos: A * (C + D) + B * (C + D), que corresponde al esquema que se muestra en la Figura 2, b. Además, debido a la multiplicación, podemos obtener la fórmula A * C + A * D + B * C + B * D, correspondiente a la Figura 2, c.
Los tres esquemas son equivalentes, es decir, se cierran en las mismas condiciones. Sin embargo, son diferentes en complejidad.
Figura 1. Circuitos de contacto típicos
El primero de los circuitos, el más simple, requiere cuatro relés, cada uno de los cuales debe tener un contacto normalmente abierto. (Para simplificar los dibujos, no se muestran las bobinas de relé).
El esquema "b" requiere un relé con dos grupos de contacto. En realidad, la tarea principal del álgebra de los circuitos de contacto es encontrar todos los circuitos equivalentes para que pueda elegir el más simple de ellos.
Figura 2. Circuitos de contacto equivalentes.
Para consolidar el material cubierto, intente resolver los siguientes problemas usted mismo.
1. Dibuje el diagrama de circuito de un autómata que tenga la fórmula estructural A * B * C * D + A * B * E + A * D.
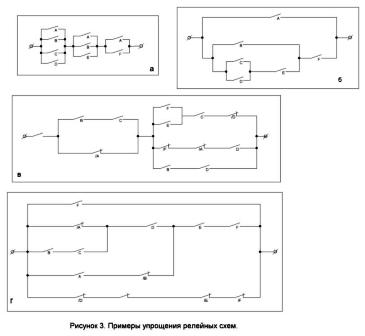
2. Demuestre que los circuitos que se muestran en la Figura 3, ayb, son equivalentes.
3. Simplifique el circuito que se muestra en la Figura 3, c.
4. ¿Qué fórmula estructural implementa el esquema en la Figura 3, d?
Después de lo que ya hemos estudiado, será posible comenzar a resolver los problemas que se establecieron al comienzo del primer artículo. Los recordamos brevemente.
La primera tarea era encender y apagar la bombilla de la habitación con tres interruptores ubicados en diferentes lugares: en la puerta, en la mesa, en la cama.
La segunda tarea es votar a los jueces deportivos: de cada cuatro jueces "FOR" deben votar al menos dos, siempre que "FOR" haya votado el presidente de la comisión.
La tercera tarea fue solo con fines educativos. Propuso lo mismo que en el primero, solo para seis interruptores, como si hubiera seis paredes en la habitación. Se están desarrollando circuitos similares utilizando el álgebra de los circuitos de relé.
En general, si queremos desarrollar un esquema que tenga algunas propiedades lógicas dadas, entonces podemos abordar este problema de dos maneras diferentes. Convencionalmente, estos caminos se pueden llamar "intuitivos" y "algebraicos".
Algunas tareas se resuelven mejor en la primera forma, mientras que otras en la segunda. El enfoque intuitivo resulta ser más conveniente cuando el funcionamiento del circuito está controlado por muchos interruptores, pero existe cierta simetría en la disposición mutua de estos relés. Veremos que aquí un enfoque intuitivo conduce a la meta más rápido, mientras que usar el aparato de álgebra de relevos en el caso de muchas variables puede ser muy engorroso. Es útil familiarizarse con los dos enfoques posibles para resolver este problema.
Comencemos con un enfoque intuitivo. Supongamos que necesitáramos construir un circuito que estaba cerrado cuando todos los n circuitos de relé de control funcionaban.
La solución a este problema no requiere una larga deliberación: está claro que la condición se cumplirá si se interconectan secuencialmente en contactos de relé normalmente abiertos.
Del mismo modo, es obvio que para construir un circuito que se cierra cuando al menos uno de los n relés se ha disparado, es suficiente conectar n contactos de relé normalmente abiertos en paralelo.
Es fácil imaginar un circuito que se cierra cuando se activan algunos, pero no todos, los relés. Tal circuito se muestra en la Figura 4, a. A la derecha hay un diagrama que funciona según el principio de "todo o nada". Se cerrará solo cuando todos los relés se disparen o los relés estén desconectados (Figura 4, 6).
Considere ahora un ejemplo más complejo. Supongamos que hay n contactos ubicados en una determinada secuencia específica: A, B, C, D, E, F ... Construimos un circuito que se cierra cuando cualquier contacto conectado en serie k está cerrado, y solo ellos lo están. Tal esquema para los valores n = 7 yk = 3 se muestra en la Figura 4, c. El método para construir tales esquemas para cualquier otro valor de n y k está claro a partir de esta figura.
Procedemos a la construcción de circuitos de acuerdo con las condiciones dadas de su trabajo utilizando álgebra de relevos.
Como antes, las condiciones de funcionamiento del circuito siempre se establecen primero verbalmente. El diseñador, antes que nada, debe poder poner en palabras lo que quiere. Si no tiene tanta claridad, entonces ningún álgebra ayudará. Siempre debe comenzar con una declaración clara de los requisitos establecidos antes del nuevo esquema. Como en cualquier negocio, esta tarea es quizás la más difícil. Si las condiciones son lo suficientemente simples, entonces podemos escribir inmediatamente una expresión de una fórmula estructural que satisfaga estos requisitos.
Ejemplo 1 Supongamos que tenemos que construir un circuito que contenga 4 contactos A, B, C y D para que el circuito se encienda cuando el contacto A esté cerrado y uno de los otros tres contactos. En este caso simple, la operación del circuito en la escritura verbal se verá así: “El circuito debe conducir corriente si los contactos A y B están cerrados, o los contactos A y C o los contactos A y D. De acuerdo en que ahora es muy simple elaborar una fórmula estructural. Se verá así:
A * B + A * C + A * D = 1 o A * (B + C + D) = 1.
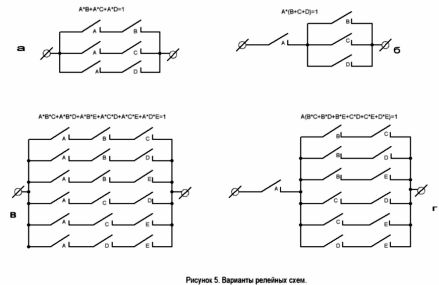
El circuito tiene dos opciones. Se muestran en la Figura 5. La segunda opción no requiere un relé con tres contactos normalmente abiertos.
Ejemplo 2 El primer artículo fue la tarea número 2 sobre la votación de los jueces deportivos. Lea su condición más de cerca, es similar al ejemplo que se acaba de examinar. Un registro verbal más claro de los requisitos se verá así: "Es necesario trazar un circuito que contenga 5 contactos A, B, C, D, E, de modo que conduzca corriente y encienda la lámpara de la pantalla si los siguientes contactos están cerrados:
A y B y C, o A y B y D, o A y B y E, o A y C y D, o A y C y E, o A y D y E. El contacto A es el botón del presidente. Si no se presiona, cada uno de los 6 productos lógicos será 0, es decir La votación no tuvo lugar.
La fórmula estructural será la siguiente:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
o A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Ambas variantes del circuito se muestran en la Figura 5, c y D. Esta es la solución al problema.
Al tener cierta habilidad para leer fórmulas estructurales, es fácil imaginar el circuito del autómata y todas sus capacidades. Curiosamente, el álgebra de los circuitos de relé proporciona más información que incluso el circuito en sí. Le permite ver cuántos y qué relés son necesarios. Con su ayuda, puede encontrar fácilmente la versión más simple de la máquina de circuitos.
Ejemplo 3 Habiendo adquirido cierta experiencia en la preparación de fórmulas estructurales, trataremos de resolver el problema que comenzó primer articulo: debe diseñar un interruptor que le permita encender la luz al entrar en la entrada y apagarla después de haber subido al piso deseado o, por el contrario, encenderla al salir del apartamento y apagarla después de bajar. La misma situación ocurre en un corredor largo: en un extremo, la bombilla debe encenderse y, después de ir al otro extremo, apagarse. En resumen, la tarea se reduce a controlar una bombilla desde diferentes lugares con dos interruptores.
Elegimos el siguiente procedimiento para resolver el problema: primero, formulamos claramente las condiciones de funcionamiento de los interruptores, luego los escribimos en forma de fórmula y dibujaremos un circuito eléctrico basado en ellos.
Entonces, que la bombilla se quemó (1), es necesario que se cumpla una de dos condiciones:
1. Encienda el interruptor en la parte inferior (A) y apáguelo en la parte superior (/ B). Entra al porche.
2. Encienda el interruptor en la parte superior (B) y apague la parte inferior (/ A). Salga del apartamento.
Usando la notación aceptada, la fórmula estructural se escribe de la siguiente manera:
A * (/ B) + (/ A) * B = 1
El diagrama del circuito del interruptor se muestra en la Figura 6. Actualmente, tales interruptores están disponibles comercialmente, estos son los llamados interruptores de paso. Por lo tanto, la consideración de estos esquemas aquí se da simplemente por el concepto de los principios generales de su trabajo.
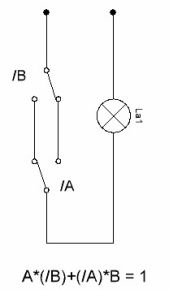
Figura 6
En la tarea No. 1 al comienzo del primer artículo, estábamos hablando de un esquema que le permite encender y apagar la luz en la habitación con cualquiera de los tres interruptores. Razonando de la misma manera que en el caso de dos interruptores, obtenemos la fórmula estructural:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
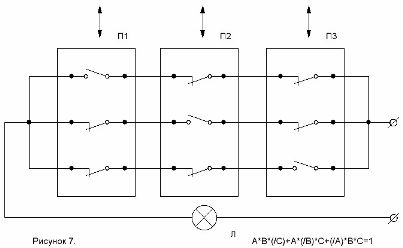
El esquema elaborado por esta fórmula se muestra en la Figura 7.
Figura 7
Al comienzo del primer artículo, se propuso una tarea educativa simple No. 2: como si hubiera seis paredes en la habitación y cada una tuviera un interruptor. La lógica del circuito es exactamente la misma que para los tres interruptores. Denotémoslos con las letras A, B, C, D, E, F. Recuerde que la notación (/ A), (/ B), etc., no es un signo de división, sino una negación lógica. Con mayor frecuencia se indica subrayando caracteres e, incluso, expresiones completas, en la parte superior. En algunos esquemas, este guión bajo simplemente se reemplaza por un signo menos. Entonces, la fórmula estructural para los seis interruptores es:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C * *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Se invita a los lectores a elaborar un circuito eléctrico completo que implemente esta fórmula estructural para adquirir habilidades prácticas en el diseño de circuitos. Una pequeña pista: para el circuito necesitará seis relés, cada uno de los cuales tiene un contacto normalmente abierto y cinco normalmente cerrados. Tales relés complejos, si es necesario, se pueden ensamblar a partir de varios más simples conectando sus bobinas en paralelo.
Esto concluye la historia del álgebra booleana y el álgebra de los circuitos de relé.
Continuación del artículo: Chips lógicos
Boris Aladyshkin
Ver también en electro-es.tomathouse.com
: