Álgebra booleana. Parte 1. Un poco de historia

En la escuela, todos estudiamos álgebra, pero no hablaron de álgebra booleana allí. ¿Cuál es la diferencia entre el álgebra booleana y el álgebra escolar? La historia de su apariencia, problemas y aplicaciones se describen en este artículo.

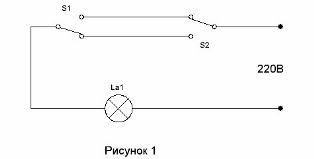
El circuito que permite que dos interruptores enciendan la luz en el pasillo a la entrada del pasillo y la apaguen al entrar en la habitación se conoce desde hace mucho tiempo (ver. Circuito de control de iluminación del pasillo) Se muestra en la Figura 1.

Tarea número 1. Más complicado Cree un diagrama que le permita encender y apagar la luz en su habitación con cualquiera de los 3 interruptores diferentes. Los interruptores se encuentran en la entrada de la habitación, encima de la cama y en el escritorio.

Tarea número 2.

En un comité de deportes, como un comité de fábrica, se reunieron 5 jueces.

Cada uno de ellos debe votar por diferentes decisiones. La decisión se adopta por mayoría de votos, pero solo bajo la condición adicional de que el presidente del comité vote por ella.

Los jueces votan presionando el botón que cierra el interruptor ubicado debajo de la mesa en la que están sentados. Cerrando el interruptor, votan a favor, desconectando los contras. Dibuje un diagrama simple que le permita ver automáticamente los resultados de la votación. En el caso más simple, simplemente con la ayuda de una bombilla - encendida - se tomó la decisión, no se encendió - no.

Tarea número 3. En la práctica, esto es poco probable, pero como una tarea educativa compleja es bastante adecuada.

En una gran sala hexagonal, se instala un interruptor en cada pared. Construya un circuito para que en cualquier momento pueda encender o apagar la luz de la habitación girando un (cualquier) interruptor.

Después de sentarse sin éxito en tareas durante tres o cuatro días, déjelos a un lado temporalmente. Y ponerse a trabajar Álgebra booleana. Es álgebra booleana o, como también se le llama, Álgebra booleana, álgebra de circuito de relé, te ayudará a resolver tus problemas.

¿Qué es el álgebra booleana?

Por extraño que parezca, a pesar de que durante cinco años han estado estudiando álgebra en la escuela, muchos estudiantes, y luego adultos, no podrán responder la pregunta, ¿qué es el álgebra? El álgebra es una ciencia que estudia los conjuntos de algunos elementos y las acciones sobre ellos.

En un curso escolar de álgebra, tales elementos son números. Los números se pueden denotar no por números, sino por letras, todos están familiarizados con esto. En las primeras lecciones de álgebra, esto siempre dificulta a muchos estudiantes. Recuerde lo difícil que fue al principio acostumbrarse a sumar letras en lugar de números, resolviendo ecuaciones que no dicen nada.

Probablemente, cada uno de nosotros se hizo la pregunta: "¿Por qué necesitamos ingresar letras en lugar de números y es necesario?" Y solo más tarde viste qué ventajas ofrece el álgebra al resolver problemas en comparación con la aritmética.

El álgebra se usa en muchas ciencias exactas. Esto es física, mecánica, sopromat, electricidad. Ley de ohmios no hay nada más que una ecuación algebraica: es suficiente sustituir sus valores numéricos en lugar de letras para averiguar qué corriente fluirá en la carga o qué resistencia tiene una sección del circuito.

Entonces te familiarizaste con el álgebra de números o con el álgebra elemental. La tarea principal y casi única es obtener una respuesta a la pregunta: “¿A qué equivale X? ¿Cuánto?

En la escuela secundaria, estudian los inicios del álgebra vectorial. Este álgebra es fundamentalmente diferente del álgebra elemental. Tiene una naturaleza diferente del conjunto estudiado y otras reglas de acción. Al resolver la ecuación del vector, obtenemos en la respuesta un vector que no es un número ordinario que responde a la pregunta "¿Cuánto?"

Las fórmulas del álgebra vectorial son en muchos aspectos diferentes de las fórmulas del álgebra elemental. Por ejemplo, en álgebra elemental y en álgebra vectorial hay una operación de suma. Pero se realiza de maneras completamente diferentes.La suma de números no es lo mismo que la suma de vectores.

Hay otras álgebras: álgebra lineal, álgebra de estructuras, álgebra de anillos, álgebra de lógica o, lo que es lo mismo, álgebra booleana. Probablemente no escuchaste el nombre en las clases de la escuela. George Boole - pero todos saben el nombre de una de sus talentosas hijas Ethel Voinich (1864 - 1960). Ella escribió la novela "Gadfly", que cuenta sobre la lucha por los derechos de los carbonarios italianos.

George Bull nació en Inglaterra el 2 de noviembre de 1815. Toda su vida trabajó como profesor de matemáticas y física en la escuela. De las memorias de sus alumnos se sabe la gran importancia que Bul atribuía al desarrollo de las habilidades creativas de los alumnos. Al presentar material nuevo, trató de asegurarse de que sus propios estudiantes "redescubrieran" ciertas fórmulas y leyes.

Al contarles a los estudiantes sobre las dificultades que los científicos enfrentaron inevitablemente en la búsqueda de la verdad, al maestro le gustaba repetir una sabiduría oriental: incluso el trono persa no puede brindarle tanto placer a una persona como el descubrimiento científico más pequeño. Buhl nunca perdió la esperanza de que algún día sus estudiantes harían un verdadero descubrimiento.

La gama de intereses científicos de Buhl era muy amplia: estaba igualmente interesado en las matemáticas y la lógica, la ciencia de las leyes y las formas de pensamiento. En aquellos días, la lógica se consideraba una ciencia de las humanidades, y muchos de los que conocían a George Boole estaban asombrados de cómo los métodos exactos de cognición inherentes a las matemáticas y los métodos puramente descriptivos de la lógica podrían coexistir en una persona.

Pero el científico quería hacer que la ciencia de las leyes y las formas de pensamiento fuera tan rigurosa como cualquiera de las ciencias naturales, dicen las matemáticas y la física. Para esto, Boule comenzó a denotar no números como letras, como se hace en álgebra ordinaria, sino declaraciones, y demostró que tales ecuaciones, muy similares a las algebraicas, pueden resolver preguntas sobre la verdad y la falsedad de las declaraciones hechas por el hombre. Entonces surgió el álgebra booleana.

Pero mucho antes de George Buhl, al matemático y filósofo alemán Gottfried Leibniz (1646-1716) se le ocurrió la idea de crear una ciencia que designara todos los conceptos del discurso coloquial ordinario con símbolos y estableciera un nuevo álgebra para combinar estos símbolos.

Después de la creación de tal ciencia, según Leibniz, los científicos y filósofos dejarán de discutir y gritarse unos a otros, descubriendo la verdad, pero tomarán un lápiz y con calma dirán: "¡Calculemos!"

Hoy, el álgebra de la lógica se ha convertido en una parte importante de las matemáticas. Una de sus tareas es la solución de todo tipo de ecuaciones, cuyas relaciones numéricas se reemplazan por letras. Probablemente, cada uno de ustedes a lo largo de su vida recordó cómo resolver ecuaciones de segundo y tercer grado con coeficientes de letras. Entonces, Boole en su nuevo álgebra utilizó todas estas fórmulas y reglas.

Lo nuevo en el álgebra booleana es que los elementos del conjunto que se estudian en él no son números, sino enunciados. Si, al resolver ecuaciones algebraicas ordinarias, se determina qué número es igual a X desconocido, el álgebra escolar busca la respuesta a la pregunta: "¿Cuánto?"

El álgebra de la lógica está buscando la respuesta a la pregunta: "¿Es esta o aquella afirmación denotada por la letra X verdadera?"

El significado y el contenido de la declaración no juegan ningún papel aquí. Cada declaración solo puede ser verdadera o falsa. No puede ser mitad verdadero y mitad falso. Como ejemplo, podemos recordar lanzar lotes con una moneda.

Solo se consideran dos estados de monedas: cara o cruz. Por acuerdo de las partes, el águila es SÍ, y las colas son NO. No se tienen en cuenta otros puntos intermedios en la teoría de la probabilidad, aunque son posibles. Una moneda lanzada puede caer sobre un borde, rodar por el piso hasta las patas de una silla o mesa y permanecer en posición vertical, o incluso caer en un amplio espacio en el piso. (Por analogía con los circuitos eléctricos, las dos últimas situaciones pueden considerarse un mal funcionamiento en forma de contacto quemado).Pero en aquellos días, el álgebra booleana, por desgracia, no se usaba ampliamente.

Claude Shannon "descubrió" el álgebra de Buhl nuevamente. En 1938, cuando todavía era estudiante del Instituto de Tecnología de Massachusetts y América, el joven Claude demostró que el álgebra booleana es completamente adecuado para el análisis y la síntesis de los circuitos de relé y conmutación.

Con la ayuda del álgebra booleana, es muy fácil hacer un circuito eléctrico de un autómata que opera en un relé.Para esto, resulta que solo necesita saber exactamente qué debe hacer la máquina, es decir, debe tener un algoritmo para su funcionamiento. Por lo tanto, se sentaron las bases para la teoría de las máquinas digitales que funcionan según el principio de SÍ o NO.

Tal, en resumen, es la historia del álgebra booleana. En los siguientes artículos consideraremos sus leyes básicas, ejemplos de circuitos de contacto que implementan estas leyes. Considere la solución de esas tareas que se dieron al comienzo del artículo.

Continuación del artículo: Álgebra booleana. Parte 2. Leyes y funciones básicas.

Boris Aladyshkin