"Todo fluye", o la Ley de Ohm para los curiosos

Incluso el último holgazán, después de haber estudiado durante algún tiempo en el décimo grado, le dirá al maestro que Ley de ohm - esto es "U es igual a I por R". Desafortunadamente, el mejor estudiante inteligente dirá poco más: el lado físico de la ley de Ohm seguirá siendo un misterio para él durante siete sellos. Me permito compartir con mis colegas mi experiencia al presentar este tema aparentemente primitivo.

El objeto de mi actividad pedagógica fue el décimo grado de arte y humanitario, cuyos intereses principales, como adivina el lector, estaban muy lejos de la física. Es por eso que la enseñanza de este tema fue confiada al autor de estas líneas, quien, en general, enseña biología. Fue hace unos años.

La lección sobre la ley de Ohm comienza con la declaración trivial de que la corriente eléctrica es el movimiento de partículas cargadas en un campo eléctrico. Si solo una fuerza eléctrica actúa sobre una partícula cargada, entonces la partícula se acelerará de acuerdo con la segunda ley de Newton. Y si el vector de fuerza eléctrica que actúa sobre la partícula cargada es constante en toda la trayectoria, entonces es igualmente acelerado. Al igual que un peso cae bajo la influencia de la gravedad.

Pero aquí el paracaidista cae completamente mal. Si descuidamos el viento, entonces su tasa de caída es constante. Incluso el estudiante de la clase de arte y humanitario responderá que, además de la fuerza de la gravedad, otra fuerza de caída actúa sobre el paracaídas que cae: la fuerza de la resistencia aérea. Esta fuerza es igual en valor absoluto a la fuerza de atracción del paracaídas por la Tierra y es opuesta a ella en dirección. Por qué Esta es la pregunta clave de la lección. Después de una discusión, concluimos que la fuerza de arrastre aumenta al aumentar la tasa de caída. Por lo tanto, el cuerpo que cae acelera a una velocidad a la cual la gravedad y la resistencia al aire se igualan, y el cuerpo cae aún más a una velocidad constante.

Es cierto que en el caso de un paracaidista, la situación es algo más complicada. El paracaídas no se abre de inmediato y el paracaidista acelera a una velocidad significativamente mayor. Y cuando el paracaídas ya se abrió, la caída comienza con una desaceleración, que continúa hasta que la fuerza de la gravedad y la fuerza de la resistencia del aire se equilibran.

Para una carga de paracaídas con una masa total m que desciende a una velocidad constante v, podemos escribir: mg - F (v) = 0, donde F (v) Es la fuerza de resistencia del aire, considerada como una función de la velocidad de caída. En cuanto a la forma de la función F (v) hasta ahora solo podemos decir una cosa: está creciendo de manera monótona. Es esta circunstancia la que proporciona la estabilización de la velocidad.

En el caso más simple, cuando F (v) = k, la velocidad constante con la que caerá el paracaídas será igual a mg / k. Hagamos algo de conversión ahora. Deje caer el paracaídas desde una altura h. Entonces, la diferencia en las energías potenciales del cuerpo antes y después de la caída será igual a mgh = mU, donde U es la energía potencial del cuerpo de la unidad de masa a una altura h, o la diferencia de potencial del campo gravitacional en los puntos de incidencia inicial y final.

En vista de lo anterior, obtenemos la fórmula: F (v) = mU / h. (1)

Y ahora de vuelta al conductor a través del cual fluye la corriente eléctrica. Una gran cantidad de partículas cargadas se mueven a lo largo del conductor, que colisionan con los átomos con mayor frecuencia cuanto más rápido vuelan. La analogía con el descenso de un paracaídas es bastante transparente, la única diferencia es que hay muchos "paracaídas" y no se mueven en el campo gravitacional, sino en el eléctrico. Dadas estas circunstancias, (1) puede reescribirse en la forma: F (v) = eU / l, (2)

donde e es la carga de partículas, U es la diferencia de potencial eléctrico en los extremos del conductor, l es la longitud del conductor.La intensidad actual es obviamente igual a I = neS, donde n es el número de partículas cargadas por unidad de volumen, S es el área de la sección transversal del conductor, es la velocidad de las partículas (por simplicidad, suponemos que todas las partículas cargadas son iguales).

Para obtener la dependencia I (U), debe conocer explícitamente la dependencia F (). La opción más simple (F = k) da inmediatamente la ley de Ohm (I ~ U):

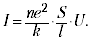
El valor se llama conductividad, y el recíproco se llama resistencia. En honor al descubridor de la ley, la resistencia generalmente se expresa en ohmios.

El valor (ne2 / k) se llama conductividad específica, y su valor inverso se llama resistencia específica. Estos valores caracterizan el material en el que consiste el conductor. Es significativo que la conductividad sea proporcional al número de partículas cargadas por unidad de volumen (n). En metales y soluciones electrolíticas, este número es grande, pero en dieléctricos es pequeño. El número de partículas cargadas por unidad de volumen de un gas puede depender del campo aplicado (es decir, es una función de U); por lo tanto, la ley de Ohm no se aplica a los gases.

Al derivar la ley de Ohm, hicimos una suposición no obvia. Aceptamos que la fuerza que inhibe el movimiento de una partícula cargada es proporcional a su velocidad. Por supuesto, uno podría tratar de justificar esta idea de alguna manera, pero la verificación experimental parece mucho más convincente.

Una verificación experimental de este supuesto es, obviamente, una verificación de la propia ley de Ohm, es decir. proporcionalidad de U e I. Parece que esto no es difícil de hacer: ¡tenemos un voltímetro y un amperímetro! Por desgracia, no todo es tan simple. Tenemos que explicar a nuestros estudiantes que un voltímetro, al igual que un amperímetro, no mide el voltaje, sino la intensidad de la corriente. Y tenemos derecho a poner voltios en la escala de un voltímetro solo porque inicialmente conocemos la ley de Ohm, que queremos verificar. Necesita otros enfoques.

Puede, por ejemplo, usar la siguiente idea. Conectamos n baterías en serie y suponemos que el voltaje en este caso aumentó n veces. Si la ley de Ohm es verdadera, entonces la intensidad actual también aumentará n veces, por lo que la relación n / I (n) no dependerá de n. Esta suposición se justifica por la experiencia. Es cierto que las baterías también tienen resistencia interna, por lo que el valor de n / I (n) crece lentamente al aumentar n, pero no es difícil de corregir. (G. Ohm mismo midió el estrés de una manera diferente, sobre la cual los estudiantes pueden leer en el libro de texto de G.Ya. Myakishev y otros).

Hacemos la pregunta: "" En la lejana constelación de Tau Ceti ", no la ley de Ohm, sino la ley del gran científico local Académico X. Según la ley de X, la fuerza actual es proporcional al cuadrado de la diferencia de potencial en los extremos del conductor. ¿Cómo depende la fuerza de frenado de las partículas de su velocidad en el Tau Ceti? Con la ayuda de transformaciones simples, los estudiantes llegan a la conclusión de que la fuerza es proporcional a la raíz cuadrada de la velocidad.

Y ahora pasemos a otro proceso: el movimiento del agua en una tubería, en cuyos extremos se crean diferentes presiones. Aquí tenemos una situación completamente diferente: no se frotan las partículas móviles separadas contra un material estacionario distribuido en todo el volumen del conductor, sino que las capas de partículas móviles se rozan entre sí. Y esta circunstancia cambia fundamentalmente todo razonamiento físico.

Dos fuerzas actúan sobre una capa separada de agua que se mueve en una tubería:

a) la diferencia en las fuerzas de presión en los extremos de la capa;

b) la fuerza de fricción contra las capas vecinas de agua.

Si se establece una velocidad constante de la capa, entonces estas fuerzas son iguales y se dirigen en direcciones opuestas.

La fuerza de fricción contra las capas de agua vecinas puede ralentizar el movimiento si y solo si diferentes capas de agua se mueven a diferentes velocidades. En un conductor, la velocidad de las partículas cargadas no depende de si están en el borde del conductor o en su centro, pero el agua en el centro de la tubería se mueve rápida y lentamente a lo largo de los bordes, en la superficie misma de la tubería, la velocidad del agua es cero.

Un análogo de la intensidad actual puede considerarse flujo de agua, es decir. La cantidad de agua que sale de la tubería por unidad de tiempo. Dado que la velocidad del agua en diferentes capas no es la misma, calcular el caudal no es tan simple.Un análogo de la diferencia en los potenciales eléctricos es la diferencia de presión en los extremos de la tubería.

Al igual que en un conductor con corriente, se observa una proporcionalidad directa en la tubería con agua entre la diferencia de presión en los extremos y el caudal. Pero el coeficiente de proporcionalidad es completamente diferente. Primero, el caudal de agua depende no solo del área de la sección transversal de la tubería, sino también de su forma. Si la tubería es cilíndrica, entonces la velocidad de flujo es directamente proporcional, no al área de la sección transversal, sino a su cuadrado (es decir, el radio al cuarto grado). Esta dependencia se llama ley de Poiseuille.

Este es el momento de recordar el curso de anatomía, fisiología e higiene, estudiado en el noveno grado. El cuerpo humano tiene una gran cantidad de vasos conectados en paralelo. Supongamos que uno de estos vasos se ha expandido y su radio ha aumentado ligeramente, solo dos veces. ¿Cuántas veces, con la misma presión en los extremos del vaso, aumentará la cantidad de sangre que lo atraviesa? El área de la sección transversal es proporcional al cuadrado del radio, y el cuadrado del área de la sección transversal es proporcional al radio de cuarto grado. Por lo tanto, cuando el radio se duplica, el flujo sanguíneo aumenta 16 (!) Veces. Tal es el poder de la ley de Poiseuille, que nos permite crear un mecanismo muy efectivo para redistribuir la sangre entre los órganos. Si los electrones no fluyeran a través de los vasos sanguíneos, pero su flujo aumentaría solo cuatro veces.

La descripción del tema descrito anteriormente es diferente de la tradicional. En primer lugar, se dedican tres lecciones al tema, que, con la escasez actual de horas, puede considerarse un lujo inadmisible para las ciencias naturales. Sin embargo, esto se justifica por el hecho de que es posible revelar de manera simple y popular el significado físico de la ley y equipar a los estudiantes con una metodología que pueden usar para analizar una variedad de procesos físicos: la caída de un cuerpo en el aire, el movimiento de un fluido en una tubería, el movimiento de partículas cargadas a lo largo de un conductor, y más tarde en el análisis del paso de la corriente eléctrica a través del vacío y los gases.

Este enfoque se llama integración intradisciplinaria. Con su ayuda, demostramos a los estudiantes características comunes en las distantes, a primera vista, secciones de física, mostramos que la física no es un "grupo" de "leyes físicas" que no están conectadas entre sí, sino un edificio delgado. Lo mismo es cierto, por supuesto, para otras disciplinas científicas. Y así, al parecer, una pérdida irracional de horas de entrenamiento está dando sus frutos.

Lee también:Cómo usar un multímetro