¿Cuál es la conexión entre las secciones de alambre y la población de conejos?

En 1202, el matemático italiano Leonardo Fibonacci publicó su trabajo bajo el título de "Libro de ábaco" ("Libro de cálculos"), en el que también describió series de números inmortalizados por su nombre. En uno de los capítulos, Fibonacci intenta mostrar matemáticamente cómo aumentará la cantidad de conejos. Consideró las siguientes hipótesis como condiciones:

1) los primeros dos meses un par de conejos no dan descendencia;

2) a partir del tercer mes, un par de conejos da otro par de conejos.

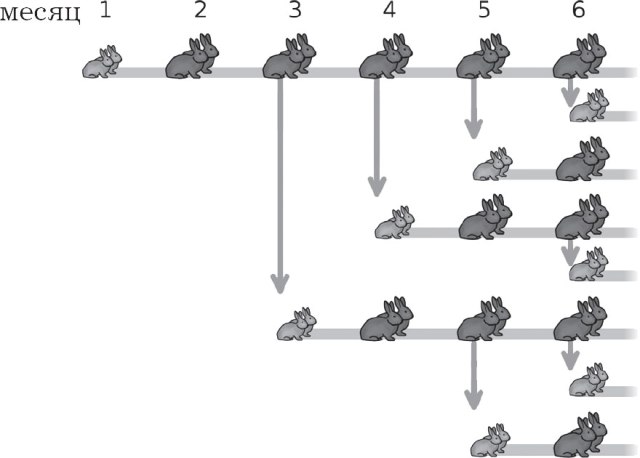
Como resultado de construir un patrón de crecimiento de la población de conejos, obtenemos la siguiente serie de números, notando el aumento en el número de conejos cada mes:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

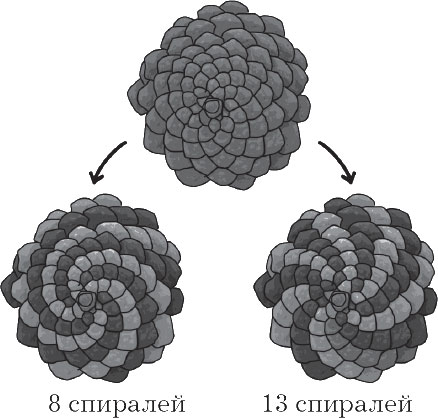
Si observa cuidadosamente la protuberancia, verá que su superficie consiste en escamas que se tuercen en espiral de acuerdo con la secuencia de Fibonacci. Mientras están en piña o en una flor de girasol, son visibles a simple vista.

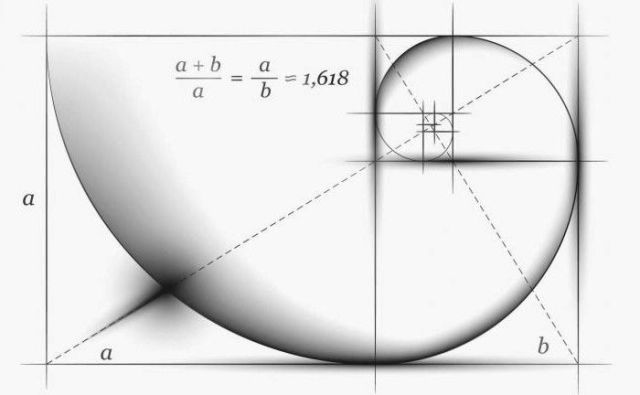
Desde la época de la antigüedad de la proporción áurea, el número = 1.618. Los antiguos griegos consideraban el valor de la proporción ideal. La proporción áurea es la proporción de cada número subsiguiente en la serie de Fibonacci al anterior:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

Los antiguos griegos lo usaban en arquitectura. La fachada del Partenón en Atenas tiene proporciones muy similares con un rectángulo construido según el principio de la proporción áurea.

Entonces, ¿cuál es la belleza de la secuencia de secciones transversales de cables, corrientes nominales de corrientes eléctricas y de corte de interruptores automáticos? Construya una serie de números con los siguientes valores: 1,5; 2.5; 4; 6; 10; 16; 25; 40; 63...

Corrientes clasificadas de arrancadores electromagnéticos:

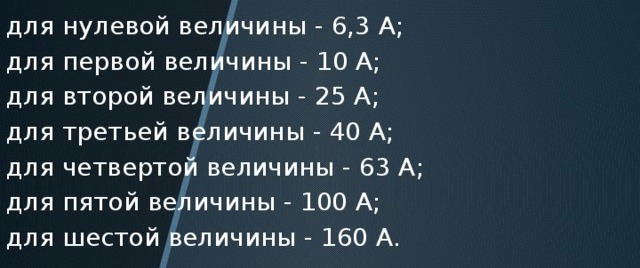
Entonces, si divide 2.5 / 1.5; 4 / 2.5; 6.3 / 4; 10 / 6.3; 16/10; 25/16; 40/25; 63/40entonces obtenemos alrededor de 1.6. Que corresponde a la regla de la proporción áurea. Y refleja la belleza y el genio de la naturaleza incluso en nuestros aburridos sistemas de ingeniería.

Que piensas ¿Es esto un accidente?

Basado en el libro "Una gran novela sobre matemáticas. Historia del mundo a través del prisma de las matemáticas" de Michael Lone. Gracias por la recomendación de Vladimir Kisel.

Alexey Bushnyaga